强化学习 -Part 2:Modern Methods
上一篇 强化学习-Part 1:From MDP to DQN 我们介绍了强化学习的基本问题,MDP 建模方法,以及 value-based 的强化学习方法。这些方法我归类为传统方案,其中 DQN 方法在 2014 年在雅达利游戏中超过人类选手。本文介绍的 Policy based 以及 Actor-Critic 方法是现在强化学习的主流方法。当然这些方法也大量使用了 value-based 的想法,以及我们上一篇文章介绍的 MC、TD-Learning 等随机近似的方法。
本篇文章,我们会先讨论基于 Policy 的 Policy gradient 方法,REINFORCE。然后讨论 policy 和 value 结合的 actor-critic 方法。基于此,我们会进一步讨论 TRPO 和 PPO 这些现代方法。
我们首先回顾一下,在 MDP 模型的设置下,我们使用了贝尔曼公式和贝尔曼最优公式描述了 state、 action value 的关系。为了估计 value 的值,使用 MC 方法进行估计,或者使用 TD-Learning 来渐进式的估计 value,最后引入 value function 刻画连续状态下的 value 值。利用神经网络强大的泛化性来拟合 value。所有的一切围绕讨论如何求解 value,我们期望求得 action value
Policy-based 方法的基本想法是:我们能不能直接求得策略 Policy,而不是通过先求 action value,再求 policy。
如何直接获得 policy 呢?非常类似优化 value function 的思路,我们还是使用梯度下降的想法。首先定义一个基于 policy 的损失函数(也叫 metrics),然后优化(最大化)这个 metrics,当遇到未知变量的时候,我们尝试用“近似值”替代。
Policy Gradient
为了直接求解 policy,我们定义 policy 为下面的式子,不同于之前的定义
这里的策略可以用一个神经网络来表示,他的输入是状态,输出是 action,模型的参数是
在上一篇文章中策略定义为
,之所以没有参数 , 是因为我们的策略不需要参数,他要不是从 里面 greedy 求出,要不是结合 ε-greedy 策略给出。
我们定义,和策略相关的 metric,目的是“只要优化 metrics,是得 metrics 最大,我们就能得到最优的策略”
Metrics
Metric 1:Average state value
- 这是对所有 state value
的加权和。其中 是状态 的 weight 权重 且 - 最简单的情况是均匀分布,每个状态的概率相同
- 如果
的分布与策略 无关,我们可以把这个特殊情况的 metric 记为 - 另外一种情况是“稳态分布”(stationary distribution),指的是执行多次(无数次)策略最后收敛到的“状态被访问到的概率”
- 也可以表达为:
Average value 的一个等价表达:discounted reward (折扣回报)的期望。
注意,换个角度理解,这个损失函数可以看作是所有路径 trajectory 的 discounted Return 的加权和(即,期望
)
Metric 2:Average one-step reward
- 这里是对所有状态“immediate reward“的加权和。
的定义是 状态下执行所有 action 的 immediate reward 的期望,即 - 这里的
是状态 下执行某个具体动作 的当下的奖励。他也可能是一个随机变量,
Average reward 的一个等价表达: reward 的均值的期望
- 这里的
两个 metrics 可以相互转换
求梯度
我们再回忆一下我们的目标:希望找到一个策略使得上面的 metric 最大化。
基本思路:下面的推导思路与我们上一篇文章中的 value 的函数近似类似。在 metric/损失函数的基础上求导,进行梯度上升/下降。我们会把求梯度后的形式转化为期望的形式(Expection,
基于上面的基本思路,我们观察上面的 metric 公式,有一个“小问题”,上面 metric 的定义都是基于 Reword,我们需要把他们展开为 value(
可以对对比 value 的函数近似那里直接就是 state Value,可以直接应该 rm,这里就需要对公式镜像展开化简。
对上面的 metric 求梯度,直接给出一个通用的解如下所示(他适用于上面所有的 metric):
上面第一行到第二行的推导里面这里使用到的一个 log 的导数的公式,我们通过他把梯度最终转化为了“期望”的形式。
这一步推导如下(简而言之,就是从公式里面提取出 state
上面我们直接给出了梯度的结论,他是如何导出的呢?下面内容作为参考:
针对 metric这可以有两种表述,他们是等价的:
- 训练一个 Policy
例如神经网络,在所有的 Trajectory 中,得到 Return 的期望最大。 - 寻找一个 Policy
例如神经网络,在所有状态 下,给出相应的 Action,得到 Return 的期望最大。
为了把把公式转化为包含策略的形式 我们需要把上面的“1”转化为 “2”: - 求梯度:
- 轨迹概率
可分解为初始状态分布和策略的乘积: - 求 2 中的轨迹概率的梯度,
- 3 代入 1 中:
- 重点理解这里的
表示的是一个轨迹 Trajectory 的奖励之和 ,他是长期累计奖励(Discounted Reward)随机变量 的一个采样(Sample), - 由于
只是一个采样,所以可能非常不稳定,variance 非常大, - 实践中,我们一步只要考虑时间
之后的 reward 就行, 之前的 reward 应该对当前 action 没有影响。即 修改为 - 考虑
在这里非常的不稳定,是使用 即轨迹 return 的期望,而不是轨迹 return 的采样来作为 , 就是 的定义! - 最终我们得到了上面的公式
基于上面的梯度公式的期望形式,使用 RM 算法迭代估计求解
根据这个迭代公式,只要我们有后面的采样值就能一步一步的求解出
理解 gradient
分析上面公式的 intuition,首先我们尝试理解里面的
角度一:展开
如果我们不用
角度二:如果再仔细观察策略梯度的更新公式
其实再 ML 中,我们还有一个常见的任务,多分类的交叉熵包含
对于某个样本而言,只有一个
我们可以把学习的策略也看作一个多分类问题(classification task),于是策略梯度的公式可以解释为使用 action value 加权的多分类 loss
角度三:另外一个现实意义的 intuition 是,我们稍微变形一下:
如此整理后,这个方程可以看成是对策略
- 分子部分是 action value,如果一个 action 的 value 越大,则调整
赋予 action 更大的输出概率,这是鼓励利用学习的知识,即 exploit - 分母部分是当前的策略 policy,如果当前策略下
的概率较小,则调整 赋予 action 更大的输出概率, 这是估计对探索不足的 action 更多探索,即 explore。
REINFORCE
回忆上一小结,我们通过对 metrics 的参数
在这个公式中,我们对
- 使用 MC 估计
- 使用 TD Learning 方法估计
当使用 MC 估计的时候就是本节的 REINFORCE 算法。

- 这个算法是一个 online 方法(incremental),因为使用了 MC,我们需要收集完整的路径(sample 到结束,terminate state)才能估计
。 - 这个算法是一个 on-policy 算法,behavior policy是我们 follow 策略
,target policy 也是更新同一个策略的参数 。 - 值得注意的是:我们 sample 一条 episode 之后,会对路径上的所有的
进行估计(value update),也会工这些估计来进行多谢的 policy update。(更高效一些的计算方法是 episode 的后面向前计算每个 ,即 是从 到 0) - 策略不需要ε-greedy,因为
本身就是个分布,具有探索的特性
Actor-Critic 算法
上一节我们提到也可以使用 TD Learning 的方法来估计
- 这里面我们更新的策略就是 actor,是他发出了 action
- 这里面的
就是 critic,他的作用是对 action state 对 quality 进行了评估
QAC
最简单的 Actor-Critic(QAC) 算法也很直接,就是同步使用 SARSA 算法估计 quality

- 这是一个 online 算法
- 这是一个 on-policy 算法,可以看到算法中的 behavior policy 是 follow
. - 策略不需要ε-greedy,因为
本身就是个分布,具有探索的特性
A2C
引入 Advantage 的概念,其核心是在我们的策略梯度的定义中(Expection 形式)引入了 baseline 的概念
上面公式中的
Baseline 的选择,最优的 baseline 比较复杂,我们忽略,一般选择 state value,即
因此,我们有了一个更直观的解释:这里的 Critic 的评估标准是:一个 action 的 quality(
)是不是是这个状态的平均质量 ( ) 高?
简单的代入 baseline,参数的梯度上升公式:
其中,我们定义
是 Advantage Function。(优势函数)
使用随机近似的梯度更新的公式如下:
如理解 Gradient 同样的方法,我们也可以像下面这样理解这个更新公式
可以看到这里的 stepsize 理解也是从 exploit-explore 框架入手,这里 Advantage function 扮演了 exploit 的角色
最后一个问题,由于上面的 Advantage function 有即有 action value
我们可以只依赖 state value

- 这里的重点是这里的 advantage function 和 td learning for state value 中的 TD ERROR 的公式一样,就提了出来,
- 依然是 on-policy 的策略
- 策略不需要ε-greedy,因为
本身就是个分布,具有探索的特性
Importance Sample
上面的 policy graident算法都是 on-policy,因为我们再推导策略梯度时候需要满足
- 这里
可以看作我们的 target policy分布, 看作 behavior policy的分布,即数据的分布。 - 这个公式告诉我们,要在
的数据上面计算 ,即计算 在 上的期望就等价于计算 在 上的期望,简单理解就是加权平均,这个权重 称为 importance weight
因此使用上的数据来估计 上的期望的公式如下:
一个常见的疑问是:上面的公式中我们需要知道
基于上面 Importance sample 原理,我们给出使用重要性采样的策略梯度
引入 Baseline 的版本的梯度是:
这里的
Baseline 版本的公式还能进一步化简,把下面的 update 公式
展开
同样的我们理解这个更新公式:
- 他的分子部分是 exploit,只有充分的利用
- 他的分母部分是固定 behavior policy,因此没有对训练的target 策略进行探索
最终的 off policy 版本的 A2C 算法的版本如下:

这个算法中
- 我们同时把 importance sample 应用到了 value estimation(TD Learning 算法中)和策略的更新算法中。这种 importance sample 算法可以应该到我们之前提到的各种 on-policy 方法中是他们变为 off-policy
- 我们需要的数据是采样的
,其实就是 episode 里面的 - 对比 TD for state value,多了当前的 action
, 因为我们 Actor 需要更新策略。 - 不同于 Sarsa,我们这里并不需要下一步 action
, 因为我们不需要计算 action value
- 对比 TD for state value,多了当前的 action
- 关于 off-policy 何时生成数据,我们可以选择直接在训练开始是 follow 策略
直接生成需要的数据。更常见的是我们利用算法 off-policy 的特征结合多种方式生成数据,例如可以选择 - 迭代 n 轮,生成一批数据
- 使用以前的旧数据 replay 训练
- 甚至向 on-policy 一样,每一步用 ε-greedy 生成数据
一个补充,上面我们假设我们的策略是有限个的 action 输出,即
例如一个多分类的神经网络,我们有 n 个策略,且我们要求这次 action 的概率全部都大于 0(不能等于 0)。
还有一种情况是,Policy 是一个固定的输出,表示连续的动作空间,即 Deterministic Actor,用表示,他只有一个输出 action,就是我们要执行的动作是什么(其他的动作的概率是 0),此时我们策略梯度的公式的形式有些不同,参考 DPG 和 DDPG 的算法。
PS:这里所说的连续动作,常用在机器人控制领域,就是如果选择了某个动作,其他的动作概率就是 0。比如动作空间是 0-30 角度的连续值,我们无法给每个值指定概率,只能输出一个具体的角度值。
Actor-Critic 优化算法
前面,我们讨论基于 Policy Gradient 的 Actor-Critic 算法(A2C),尤其是我们引入了 Importance sample 算法,得到了 off-policy A2C 算法。虽然理论上 off-policy 提高了数据的利用率, 然而 off-policy 算法在实际使用是还是会存在不稳定的问题,例如“离线数据”与当前策略相差过大,重要性采样导致了高的方差,这些问题的存在可能导致总体上并没有提升有效数据利用率,反而降低了效率。因此,在现代强化学习中,还是大量使用的一些“精心设计”的 on-policy 算法,例如 TRPO,PPO。他们通过结合一些 off-policy 的思想,达成了更强的性能。
一些优化点包括:
- 使用 on-policy 的迭代策略结合重要性采样
- 约束策略模型参数
的变化 - 优化 Advantage Function
- GAE
- Clip
TRPO && PPO
之前 On-Policy 版本的 A2C 方法,样本效率很低,我们每次 sample 完一个 episode 后只能更新一次策略参数
为什么不能直接在 On-Policy 中采样多个 episode,然后 update 多次参数呢?
因为 update 参数之后,策略参数的分布就变了,如果多次更新,旧的 episode 和新的策略就不一致了。其实这个处理方法和 off-policy 一样。
回忆我们学习的 A2C 方法, on-policy 版本策略参数的更新公式如下:
Off-policy 版本策略参数的更新公式如下:
其中
PPO/TRPO 算法流程如下:
- 初始化策略参数
- 在每一轮迭代 k 中
- 使用
与环境交互,收集训练数据集,多个 episode 的集合 - 使用
计算所有的 Advantage function - 使用策略梯度多次迭代优化目标函数
(当前 update 的参数是 ,旧的参数是 )
- 使用
上面
我们假设每一轮迭代的当前目标策略参数是
PS:如果转化为参数的 update 公式,其实和off-policy 的 A2C 的更新公式一致。
下面我们从策略梯度开始推导,加入重要性采样, 最后反推出原始的目标函数
:
- 不含 Importance Sample 的策略梯度:
- 加入 importance Sample:
- 用条件概率展开 weight,
- 这里假设了
与 相等,即在不同的策略下,状态出现的概率相同。 - 我们展开 log 的梯度,然后约掉相同的项:
- 这里是梯度,去掉求导符号反推出原始的 cost function 是
如果我们对参数
上面的约束入如同在更新时找到一块信任区域(trust region),在这个区域上更新策略时能够得到某种策略性能的安全性保证,这就是信任区域策略优化(trust region policy optim)。TRPO 就变成了一个带约束条件的优化问题,这个问题一般使用拉格朗日法来求解。实际计算比较复杂,很难优化,实际上我们还是用 PPO 比较多,经验证明,PPO 对比 TRPO 能取得类似的效果。
PPO 则是直接在
- 上面的 KL 散度计算的是不是参数
的分布的 diff,而是策略 的输出的两个分布的差异,其实实践中就是两个神经网络输出的两组概率用 KL 散度公式计算一下 - 上面的
是个动态调整的值,他调整模型需要多关注这个“差异”: - 如果
,增大 - 如果
,减少 和 是我们设定的超参数
另外一个需要说明的是 PPO 的一个变种 PPO2,他没有使用 KL 散度加入到损失函数中,而是使用 clip 方法来近似
- 如果
对这个公式理解是他通过控制优势的权重的大小来控制策略参数
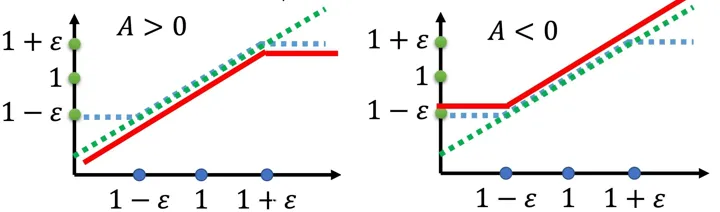
上图中 x 轴是我们通过 Importance Sample 计算出来的权重, y 轴是变化后的权重(也可以看作 Metric 大小,就是再乘以
- 如果优势函数为正数,说明执行这个 action 有正收益,我们希望
越大越好。但是我们要限制他和旧的策略 的距离不能过大,即他们权重不要大于 。防止更新参数后策略输出概率增大太多,导致和现在策略的结果太远。(对应图中,我们不让 metric 变大,直接拉平,这样梯度上升就不会再让他变大) - 如果优势函数为负数,说明执行这个 action 有负收益,我们希望
越小越好。但是我们要限制他和旧的策略 的距离不能过大,即他们权重不要小于 。防止更新参数后策略输出概率减少太多,导致和现在策略的结果太远。(对应图中,我们不让 metric 变小,直接拉平,这样梯度上升就不会再让他变小)
上面的红线直接看所 metric 函数,就是我们的优化目标,这个目标我们要控制好,不能让他过高(左图,上面的情况一),或者过低(右图,上面的情况 2)
补充 PPO 收集数据过程:
- PPO 每次迭代从多个并行环境中收集固定步数的交互数据。
- 在这些步数内,如果某个 episode 结束,环境会重置到初始状态,这个初始状态可能是随机的(取决于环境)。
- 因此,收集的数据可能包括多个 episode 的开始(从初始状态开始)以及部分未结束的 episode。
GAE(Generalized Advantage Estimation)
在上面的 Actor-Critic、PPO 算法中,使用 value function 或者 Advantage function 充当 baseline(Critic),回忆Advantage function 的定义如下:
在实际应用到时候,我们训练网络计算(直接回归)state value (
观察上面的公式,可以看出这是对优势函数的一步估计,即我们只使用了一步的 reward
从时间 t 开始,定义 1 步,2 步估计等的 Advantage function 如下:
每个时间步的 1 步估计的的 Advantage function 公式:
使用上面的 1 步估计来表示多步估计的公式:
GAE 就是上面多步估计的加权
实际在应该的时候我们怎么计算这个 GAE
- PPO 的每个迭代中的采样数据包含一段 episode(可能是部分路径,也可能完整)
- 计算episode 的长度为
,我们需要计算上面所有的 这种值 - 计算这些值的时候从 episode 后向前,逆向的方法,就是从
开始,这个计算这个 state-action 的单步 Advantage,特别地,如果这个 episode 状态恰巧是 terminate,那么优势就记为 0,
- 计算这些值的时候从 episode 后向前,逆向的方法,就是从
- 使用加权公式计算 GAE,我们可以一次从后向前计算完成这个episode 的所有
。
本质上,GAE 就是对 advantage function 的值的估计的优化,希望在方差和偏差上去得 balance,实际中,这个方法也非常有效,GAE 基本是现代 PPO 方法标配
总结
让我们自上而下的梳理本篇文章,如果要理解现代强化学习中最常用的 PPO 方法,需要我们有一些背景知识。PPO 是一种 On-Policy 的 Actor-Critic 方法,他改进自 TRPO,简化了对策略分布约束的方法。TRPO/PPO 这类方法的核心 Policy Gradient,同时结合了 Importance Sample 实现了在 on-policy 条件下更高的样本效率。此外,这类 AC 方法又要依赖我们上一篇文章中介绍的 Value Function Estimation 来实现 Critic。针对 Value 估计的改进引入了 GAE 方法。
graph TD
A["PPO(Proximal Policy Optimization)"] --> B["TRPO"]
A --> B1["GAE"]
A --> B2["KL形式损失"]
A --> B3["CLIP形式损失:PPO2"]
B --> C["Actor-Critic"]
B --> C1["Importance Sampling"]
B --> C2["KL 散度约束"]
C --> D["On-Policy Policy Gradient"]
C --> D1["BaseLine:优势函数"]
D --> E["Metric 定义"]
D --> F["理解 Gradient表达式"]
D1 --> H["Value Estimation"]
B1 --> D1
B2 --> C2
style A fill:#f9f,stroke:#333
style D fill:#bbf,stroke:#333
style C1 fill:#bbf,stroke:#333